|
|
|||||
|
Méthode de la pondération temporelle Affichage d'une grandeur instable |
 |
Maj : 14/03/06
Cette page ne peut intéresser que les développeurs d’applications de traitement de flux de données.
Si vous êtes tombés ici par mégarde, fuyez vite…
![]()
![]() Problème
de l'affichage d'une grandeur instable
Problème
de l'affichage d'une grandeur instable
Dans tout système comportant un capteur, la mesure brute est toujours irrégulière et entachée de bruit. Cela dépend évidemment beaucoup du type de mesure effectué, ce serait une mauvaise idée que d'étouffer le signal par un simple passe-bas pour le lisser.
Cette page est simplifiée au maximum pour permettre à des débutants complets de découvrir une technique très simple et utile. Les puristes en excuseront l'absence du développement mathématique nécessaire pour aller plus loin, le but n'étant pas de faire une page sur le filtrage numérique, mais simplement d'illustrer un petit cas particulier.
![]() Grandeurs
à variations très lentes
Grandeurs
à variations très lentes
Mesure de température ambiante, de pression atmosphérique …
Nous sommes ici en présence de grandeurs qui varient peu
dans le temps, un affichage de la valeur moyenne avec des délais de quelques
minutes est très stable et l'exploitation est la plus simple possible.
Lors de l'archivage des données, il n'est pas utile de stocker les valeurs
absolues qui ne varient que très peu. On utilise un stockage relatif,
à une heure donnée, une unique valeur brute est stockée,
ensuite seules les différences seront enregistrées à périodes
fixes. Mieux, le temps entre deux changements est archivé, en positif
ou négatif suivant le sens de détection d'un pas de mesure. Cette
méthode est excellente car elle restitue la totalité des données
brutes. Toutes les N mesures, pour éviter toute erreur, le cycle recommence.
![]() Signal à
variation rapide
Signal à
variation rapide
La mesure du vecteur vent est un exemple simple. Vitesse et directions changent
sans arrêt brutalement ce qui pose quelques problèmes de traitement.
En affichage analogique, c'est simple, il suffit
d'envoyer rapidement les données à l'aiguille de direction 360°
(souvent par un moteur pas à pas) et à la vitesse, un simple galvanomètre.
La mécanique intègre le bruit et l'œil accepte parfaitement
ces à-coups, le cerveau lisse à la perfection les informations.
En affichage logique, le problème est tout
autre. Il est impossible d'afficher très vite deux chiffres qui bougent
en permanence de façon pseudo-erratique. Le cerveau est totalement incapable
de les exploiter.
Il faut donc impérativement utiliser des méthodes plus subtiles,
en ne faisant que très lentement varier les chiffres avec une indication
simple de tendance. Nous allons voir quelle méthode appliquer.
Les méthodes bêtes et brutales
![]() Toutes les secondes envoyer
la valeur brute instantanée. Nous avons vu que c'est stupide et inexploitable.
Toutes les secondes envoyer
la valeur brute instantanée. Nous avons vu que c'est stupide et inexploitable.
![]() Faire la moyenne et l'afficher.
C'est un peu mieux.
Faire la moyenne et l'afficher.
C'est un peu mieux.
![]() Allonger la période
entre deux affichages. Cela fait perdre trop d'informations et n'est pas représentatif
des variations brutes.
Allonger la période
entre deux affichages. Cela fait perdre trop d'informations et n'est pas représentatif
des variations brutes.
Utiliser la méthode intelligente
C'est ce que nous allons développer dans cette page. Cela est applicable
à tout type de données, il suffit de régler les paramètres.
![]()
![]() La
méthode de la pondération temporelle
La
méthode de la pondération temporelle
Cela veut simplement dire que pour chaque nouvelle information fournie par
le capteur, la valeur reçue est comparée à l'information
moyennée précédente et à des bornes fixées,
si elle paraît aberrante, elle est affectée d'un coefficient très
faible, si elle est acceptable elle possède un coefficient élevé.
Ce coefficient de pondération représente l'indice de probabilité
de pertinence de la mesure reçue.
Pour fixer les idées, supposons que nous recevions une mesure 10 fois
par seconde.
Une bonne valeur aura un coefficient de 5% (disons 12 décimal sur une
base de 256) , une mauvaise la valeur 1/256, avec les intermédiaires
suivant la pertinence. Le microcontrôleur fait cela très simplement.
Nous allons multiplier la valeur reçue par le coefficient de pondération
(x*256) et lui ajouter la valeur précédente multipliée
par (256 *(256-x)).
Nous prenons ces valeurs car nous sommes en calculs sur 8 bits, le processeur
sait effectuer ces multiplications de base en un cycle.
Nous avons ainsi obtenu une valeur qui est 256 fois la moyenne dépendant
de l'historique.
Il suffit de décaler le pointeur pour diviser par 256 et obtenir cette
fameuse pondération temporelle.
Vous comprendrez que toute variation sera reportée et intégrée
intelligemment en tenant compte de toutes les valeurs précédentes.
Tous les réglages sont possibles en ne jouant que sur un seul coefficient.
Une donnée aura d'autant plus de poids qu'elle est plus récente,
aucune information n'est perdue.
Cette technique permet de lisser au mieux le signal en moyennant et en absorbant
les écarts brusques. C'est évidemment un passe-bas qui amènera
un retard de réponse d'autant plus grand que la pondération sera
faible
Plus x est petit, plus la réaction sera molle. Pour des flux rapides,
les coefficients ne sont pas sur 8 bits mais 16 ou 24 ce qui ne change strictement
rien sur le principe.
Dans les traitements de flux, on utilisera par exemple trois séries de données issues de la même mesure pour générer des informations statistiques très différentes :
![]() Un fort coefficient qui sera
très sensible aux variations instantanées et reflétera
la stabilité.
Un fort coefficient qui sera
très sensible aux variations instantanées et reflétera
la stabilité.
![]() Un coefficient moyen qui permettra
de suivre un signal lissé significatif et d'en déduire les variations
lentes.
Un coefficient moyen qui permettra
de suivre un signal lissé significatif et d'en déduire les variations
lentes.
![]() Un coefficient très
faible qui suivra les variations sur de très grandes durées.
Un coefficient très
faible qui suivra les variations sur de très grandes durées.
Illustrons cela par un exemple simple qui vous montrera qu'avec une seule suite d'informations donnée par un capteur, de multiples résultats et interprétations sont possibles...
![]() Mesure de
la température ambiante.
Mesure de
la température ambiante.
![]() Un fort coefficient donnera
une information rapide, il permettra de suivre la courbe sur 24h, grossièrement
une sinusoïde avec un maximum au midi solaire, un minimum la nuit.
Un fort coefficient donnera
une information rapide, il permettra de suivre la courbe sur 24h, grossièrement
une sinusoïde avec un maximum au midi solaire, un minimum la nuit.
![]() Un coefficient intermédiaire
donnera les variations sur un mois, soit trente sinusoïdes de valeurs moyenns
peu variables.
Un coefficient intermédiaire
donnera les variations sur un mois, soit trente sinusoïdes de valeurs moyenns
peu variables.
![]() Un petit coefficient montrera
les valeurs sur l'année, les variations diurnes/nocturnes seront absorbées,
la courbe sera une autre sinusoïde, maximum au solstice d'été,
minimum au solstice d'hiver, le changement de pente aux équinoxes.
Un petit coefficient montrera
les valeurs sur l'année, les variations diurnes/nocturnes seront absorbées,
la courbe sera une autre sinusoïde, maximum au solstice d'été,
minimum au solstice d'hiver, le changement de pente aux équinoxes.
![]() Un très petit coefficient
montrera la variation séculaire ou millénaire ou plus, jusqu'à
faire voir les périodes de glaciation et de réchauffement.
Un très petit coefficient
montrera la variation séculaire ou millénaire ou plus, jusqu'à
faire voir les périodes de glaciation et de réchauffement.
Tout cela avec une seule mesure en réglant un coefficient
La formulation est donc très simple :
|
Valeur (instant t) = x * Valeur capteur + ((1-x) *
Valeur pondérée (instant t-1))
|
Avec x << 1 . Le coefficient x étant très petit, pour ne pas perdre de décimales avec un microcontrôleur qui ne sait que multiplier sur 8 bits, la technique est de multiplier le deuxième terme ( "x " et "1-x ") par une grande constante, par exemple 2 16 = 65536, puis de diviser par ce coefficient après avoir effectué la somme (en shiftant) en faisant attention de faire un arrondi au plus proche pour éviter un glissement.
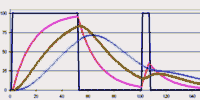
Voici le résultat de la fonction de pondération temporelle avec trois facteurs différents
Vous trouverez ici les quatre fichiers Excel ![]()
Les exemples suivants montrent la réponse à un premier signal constant, d’abord à Vcc, puis à zéro, ensuite sur une impulsion.
Tous les électroniciens ont évidemment reconnu la réponse exponentielle d’un circuit RC. Il y a une parfaite analogie. Entre les deux, le facteur Tau = RC équivalent se calcule directement avec le seul facteur de pondération.
Vous trouverez de nombreux liens en cherchant sur Google « circuit RC »
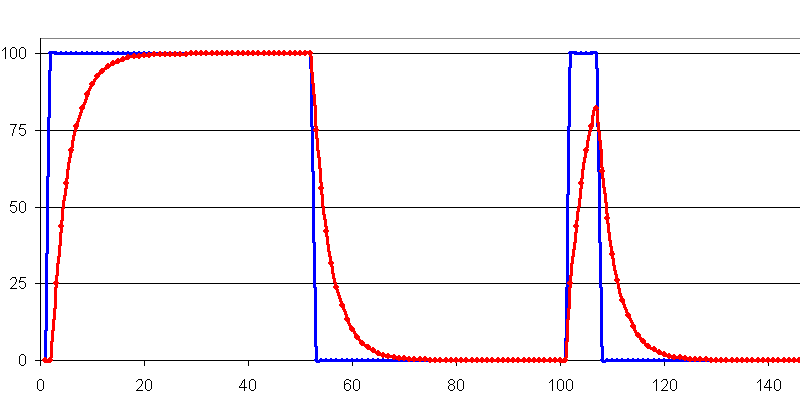
Pondération 4 : Formule Excel = (A3+(3*B2))/4
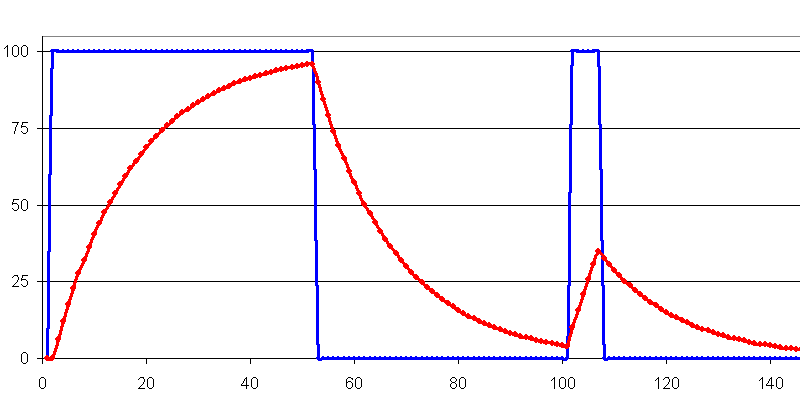
Pondération 16 : Formule Excel = (A3+(15*B2))/16
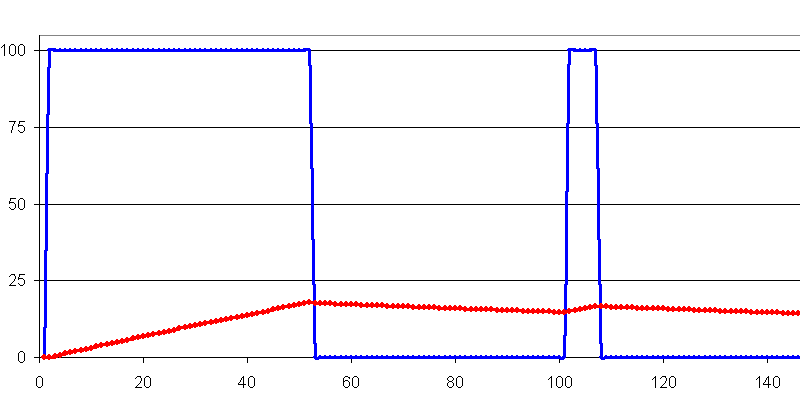
Pondération 256: Formule Excel = (A3+(255*B2))/256
![]()
![]() Implantation pratique dans un microcontrôleur
Implantation pratique dans un microcontrôleur
La mise en équation est très simple. L’astuce consiste à simplifier le problème pour n’avoir qu’une seule multiplication à faire.
Le premier terme est multiplié par un, il n’y a rien à faire, le deuxième est multiplié par un grand coefficient.
Il faut que la somme des deux soit un exposant de 2, il n’y aura par la suite qu’à diviser par ce coefficient, ce qui se fait par un simple shift.
![]() Exemples pratiques
Exemples pratiques
Pondération 4 = coefficients 1 + 3, division par 2 2 = 4, soit 2 shifts à droite
Pondération 16 = coefficients 1 + 15, division par 2 4 = 16, soit 4 shifts à droite, un nibble
Pondération 256 = coefficients 1 + 255, division par 2 8 = 256, soit 8 shifts à droite, un octet
![]() Largeur du calcul
Largeur du calcul
Supposons que la donnée à traiter soit sur 8 bits (un octet). Il est évident que la multiplication se fera sur une largeur bien plus grande afin de ne pas perdre des bits lors des arrondis
Exemple : Entrée sur 8 bits : Produit et somme sur 2 octets, la résultat étant simplement l’octet de poids fort.
En effet le plus grand nombre possible est 255+ (255*255) = 216-1= FFFFh
Généralement les capteurs ont une meilleure résolution : Données sur 16 bits calcul sur 4 octets…
![]() Méthodes par calcul ou tables
Méthodes par calcul ou tables
Il y a deux méthodes pour procéder à la multiplication avec un contrôleur qui ne sait faire que la multiplication 8 bits.
![]() Algorithme
Algorithme
Utiliser un algorithme classique qui multiplie N bits par P bits, résultat N+P bits. Cela marche parfaitement, prend peu de place mémoire, mais prend beaucoup de temps de calcul.
![]() Tables
Tables
Si le flux de données entrant est très rapide, il vaut mieux passer par une table pré calculée, en effet on multiplie toujours par le même facteur.
Pour des données 8 bits il faudra donc 256 valeurs pour l’octet haut et autant pour l’octet bas, soit 512 cases en RAM ou Eprom.
Sur 12 bits c’est plus encombrant, car nous travaillons sur 3 octets de sortie, High, Medium et Low avec 2 12 entrées = 4096, soit une occupation de 12 koctets pour les tables.
Le choix dépend des ressources et contraintes du système traité.
![]()
![]() Multiplication par soustraction
Multiplication par soustraction
Si vous ne programmez qu’en basic ou en C, vous ne vous posez aucune question existentielle, du type "que deviendrais-je après le mort", "combien de cycles machine dure ma routine", "quand est ce que ce l’on mange", "quel est la taille mémoire de mon code", "Dieu est-il amour"... ?
Si vous êtes plus performant, toutes les primitives fondamentales seront développées en assembleur, beaucoup plus rapide et compact. C’est indispensable pour des systèmes évolués. Il faudra alors mettre en œuvre des algorithmes astucieux pour réduire au maximum la taille et le temps d’exécution du code.
Nous allons prendre un exemple simple, la pondération par 256, cela vaut évidemment aussi pour tous les autres facteurs.
Nous avons supposé que notre capteur fournissait des données sur 8 bits, nous calculons sur 16 bits.
Il faut multiplier la valeur précédemment pondérée, Vt-1 par 255. C’est très gourmand en ressources.
Nous allons alors multiplier par 255 = 256-1.
La multiplication par 256 est déjà faite, car nous avons le résultat du calcul précédent en mémoire, sur 16 bits, il n’y a rien de plus à faire.
La multiplication par -1 ne prend qu’une instruction, il suffit de prendre l’octet fort du résultat précèdent et de l’inverser.
Negate (00h) donne FFh,… Negate (FFh) donne 00h.
Plutôt que d’ajouter maintenant, profitons-en pour ajouter à cet octet inversé, la nouvelle valeur Vt.
C’est une simple addition, le résultat est sur 8 bits avec un bit de retenue.
Noua ajoutons alors à l’octet faible précèdent (deux retenues), ce n’est encore qu’une simple addition 8 bits, la propagation de la retenue influe sur l’octet fort et nous avons immédiatement le résultat.
C’est magique, très propre et rapide… Il n’est pas possible de faire une routine plus performante.
![]()
![]() Récursivité
Récursivité
Cette routine est d’une grande simplicité et présente de nombreux avantages, en particulier la récursivité.
Il est très intéressant de travailler avec une pondération faible, cela prend très peu de place mémoire et de temps de calcul et de rappeler plusieurs fois la fonction.
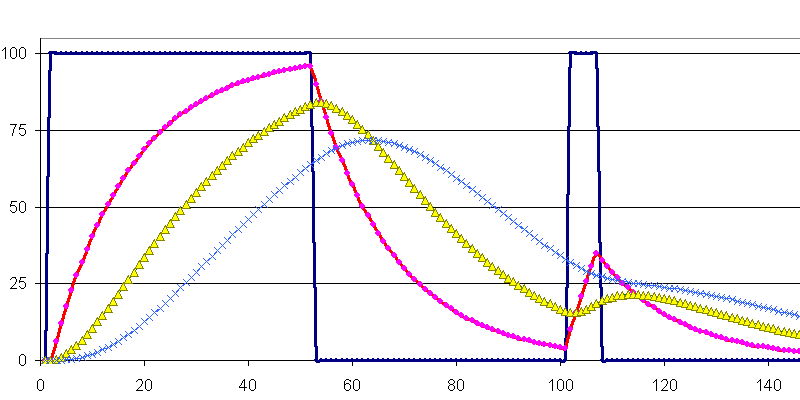
Pondération 16 avec 1, 2 et 3 passages récursifs
Cette formule Excel est un peu plus compliquée, car elle introduit directement le facteur puissance.
En faisant varier la puissance dans la case jaune, tout est instantanément recalculé !
Vous constaterez que 4 est une bonne valeur raisonnable pour cette série de données, pondération 2 4 = 16
En diminuant, ce facteur, l’efficacité du filtrage diminue.
Au-delà de 8 on ne voit presque plus de variation de la grandeur, mais cela est très utile pour les capteurs fournissant de très grandes quantités de données entre deux affichages.
La colonne B, représente le filtrage simple, courbe rose.
La colonne C, représente un filtrage à deux passes, courbe jaune.
La colonne D, représente un filtrage à trois passes, courbe bleu clair.
Vous pouvez aussi faire varier le signal d’excitation colonne A, courbe bleu foncé, en simulant des rampes, des sinusoïdes,…
![]() Exemple traitement des informations d’une girouette
Exemple traitement des informations d’une girouette
Le capteur envoie 10 données par seconde.
L’affichage se fait une fois toutes les 10 secondes.
Une pondération par 256 convient parfaitement pour un affichage de la direction instantanée.
Un deuxième passage donnera la moyenne de la direction sur la demi-heure, ce qui donne une tendance d’évolution du vent.
Un troisième passage donne la moyenne sur la semaine…
Pour les flux rapides un double passage avec coefficient de 4 convient généralement.
![]() Anémomètre
Anémomètre
C’est plus compliqué pour un anémomètre car le débit est inversement proportionnel à la vitesse, en effet, le capteur envoie N impulsions par tour, donc le filtre marchera très mal pour les vitesses très faibles car les données arrivent trop lentement, il peut y avoir des périodes d’affichage plus courtes que les périodes d’arrivées de données.
Il faut privilégier les systèmes offrant beaucoup d’impulsions par tour si l’on veut éviter les affichages instables.
![]() Application plus pertinente : Télé-surveillance d’un relais radioamateur
Application plus pertinente : Télé-surveillance d’un relais radioamateur
Les deux exemples précédents pour la mesure du vecteur vent n’étaient pas les plus représentatifs.
Prenons l’exemple d’un relais de télévision amateur en point haut, télé surveillé. Les informations sont envoyées sous formes de panneaux graphiques genre télétexte, avec une résolution assez faible.
Il est très intéressant d’afficher divers paramètres techniques pour surveiller le matériel :
![]() Tension des batteries
Tension des batteries
![]() Courant de charge de l’aérogénérateur, du panneau solaire.
Courant de charge de l’aérogénérateur, du panneau solaire.
![]() Courant consommé par le relais.
Courant consommé par le relais.
![]() Températures intérieures et extérieures.
Températures intérieures et extérieures.
![]() Temps de connexions…
Temps de connexions…
Chaque grandeur est présentée sous forme de pages défilantes, montrant les valeurs instantanées, les moyennes lentes sur la journée et très lentes sur le mois.
C’est une unique petite routine qui filtrera toutes ces données, appelée en boucle pour lisser chaque entrée de capteur.
![]() Exemple en C
Exemple en C
Voici l'application de ce principe que j’utilise pour pondérer l’information brute issue du très bon et très économique capteur de pression BMP180
const byte PONDERATION_FACTOR = 12 ; // Number of loops in low pass filter
float absolutePress = bmp.readPressure() ; // Init direct reading on BMP180
absolutePress = ((absolutePress * (PONDERATION_FACTOR - 1)) + bmp.readPressure() ) / PONDERATION_FACTOR ; // Very fast : 35 mS
![]()
![]() Conclusion
Conclusion
Un des autres avantages de cette routine pour le moyennage de données est qu’elle ne nécessite pas d’archiver une longue collection d’anciennes valeurs pour le calcul, il suffit de ne conserver que la dernière valeur traitée !
Cette méthode de la pondération temporelle, comme
tous les filtrages numériques, constitue évidemment un passe-bas
d'autant plus fort que le coefficient est petit. Par fort, il faut entendre
retard important et réponse molle.
Il est évident que si x=1, il n'y a aucun filtrage, sortie=entrée
De même si x=0, le signal d'entrée est ignoré et la sortie
est une constante.
Supposons que nous traitions un palier, valeur initiale nulle, valeur finale
constante, nous obtiendrons une courbe exponentielle, partant du zéro
au moment du saut et atteignant la nouvelle valeur au bout d'un temps infini.
C'est exactement ce que nous avons en analogique, en chargeant un condensateur
avec une résistance.
R = 0 équivaut à un coefficient x = 1
R = infini équivaut à un coefficient x = 0
Soit plus généralement, x = 1 - 1/R
Cet infini est d'autant plus rapide que le coefficient est fort.
Comme l'a dit Woody Allen : " l'infini c'est long, surtout sur la fin… "
![]()